Launching the New Year's Eve Ball into space

It can't be that hard

Every year, over a million people gather in Times Square to watch the city of New York drop the ball, literally. When you think about it, dropping the ball is a funny way to kick off a year full of new hopes and ambitious resolutions. I suggest we replace this 116-year old tradition with something more exciting, like launching it into space. If it happens to hit the International Space Station, it would be like watching the most exciting game of golf ever played.

While we could use a rocket to do this, it would be more fun to use something simpler, like a giant seesaw. The idea is that you would put the ball on one end, drop a (very) massive object on the other end, and hope that this will catapult the ball into space. If you give it a little bit of thought, it turns out that this would not be a good idea for a couple reasons.

The first problem is that in order to launch something into orbit, you have to throw it horizontally, really fast. If you’ve ever watched a rocket launch, you’ll see that the rocket gradually turns until it’s more or less parallel with the Earth. If you wanted to do this with a seesaw, it would need to swing a lot more than normal. Because the seesaw would be almost vertical, it would be difficult to drop anything onto it.

The second problem is that to accelerate the ball to the required speed, it would need to be extremely long. This is because you can only launch something as fast as gravity can pull the counterweight down, no matter how heavy a weight you use. At that point, you might as well just use a trebuchet. If you’re not familiar with trebuchets, they do almost exactly what we want: they use the energy of a falling mass to throw an object as far as possible.

Model trebuchet

Since launching the ball into space is “possible” in theory, we can figure out roughly how big of a trebuchet we’ll need and how massive the counterweight will need to be. I am going to assume that the trebuchet itself has no mass and air resistance does not exist, because this would be completely impossible otherwise. I’ll also simplify the trebuchet a bit by omitting the sling.

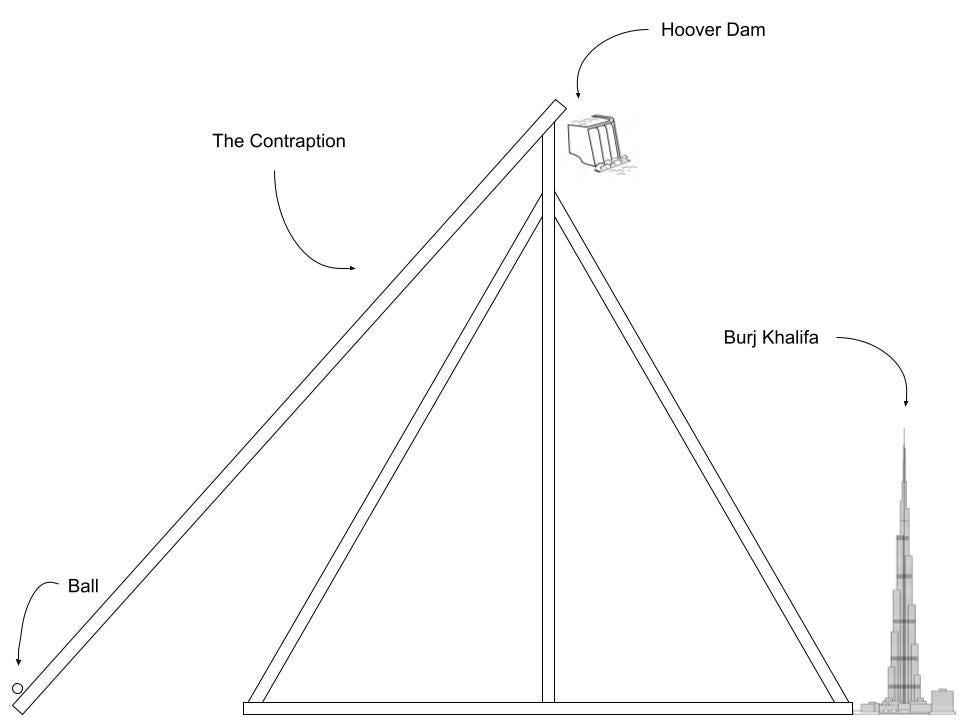
Let’s say that we want our counterweight to fall for roughly one second. This means that it will fall about 4.9 meters. Let’s also assume that the long arm of the trebuchet will make a 45 degree angle with the ground before we drop the mass. Using the equation¹ for the short arm of a trebuchet, we can find its length.

\(L_1=\frac{H_1}{1+\sin\theta}\)

\(L_1=\frac{4.9 m}{1+\frac{\sqrt{2}}{2}}=2.87m\)

A length of about three meters isn’t too bad. The long arm, however, is a different story. We need to get the New Year’s Eve ball moving at roughly 11,200 m/s before it’s released², and we only have one second to do this. The ball will experience well over 1,000 Gs of acceleration, which would definitely be enough to flatten it to a pancake.

If it doesn’t completely disintegrate, we’ll be launching a sort of frisbee-like object into space at best. Based on the ball’s average velocity, the initial angle of the long arm, and the fact that the ball traces out roughly a circular path before launch, we can work out just how long the long arm should be.

\(L_2=\frac{v_ft}{\pi+2\theta}\)

\(L_2=\frac{(11,200m/s)(1s)}{\pi+\frac{\pi}{2}}=2,376.71m\)

A length of 2,400 meters is about 1.5 miles, which presents obvious problems. However, since our trebuchet is made of a hypothetical material that has no mass and is infinitely strong, we can safely ignore this issue. Now that we have the length of the long arm and its angle relative to the ground, we can calculate how tall the trebuchet base needs to be. The base is responsible for holding the whole thing together and allowing the arm to swing freely, so it is quite important.

\(H_T=L_2\sin\theta\)

\(H_T=(2376.71m)(\frac{\sqrt{2}}{2})=1,680.59m\)

The base alone will be about twice the height of the Burj Khalifa, which again, is a big problem. However, there is never a problem so big that you cannot ignore it. Finally, we need to figure out how high the ball frisbee will be right before it’s released. This is because trebuchets actually waste some energy just by lifting the object you’re trying to throw, meaning we’ll need to compensate for this energy loss later on. To find its final height, we can just add the lengths of the base and the long arm.

\(H_2=L_2+H_T\)

\(H_2=2376.71m+1680.59m=4,057.3m\)

This means that the “ball” will be released at an altitude roughly equivalent to half that of a commercial airliner. After all of this, we can finally figure out how heavy our counterweight needs to be.

\(m_1=\frac{m_2(\frac{1}{2}{v_f^2}+H_2g)}{H_1g}\)

\(m_1=\frac{(5,386.41kg)((\frac{1}{2})(11,200m/s)^2+(9.81m/s^2)(4,057.3m))}{(4.9m)(9.81m/s^2)}\)

\(m_1=7,032,599,506.95kg\)

It turns out that this is a little over the mass of the Hoover Dam, which is 6.6 billion kilograms. Needless to say, trying to build this would be a very bad idea.

Even if we somehow managed to trick government officials into letting us use their dam for “science”, the New Year’s Eve frisbee wouldn’t even make it into space.

Moving a flat disc at Mach 32 would cause it to burn up in the atmosphere, resulting in a fiery cascade of metal and glass as it is launched from the trebuchet. There would also be a sonic boom caused by the remnants of the ball breaking the speed of sound, which would be bad news for anyone in the vicinity.

In other words, we have found a way to create the most expensive, dangerous, and potentially lethal New Year’s Eve fireworks ever conceived. Happy new year!

1. http://www.benchtophybrid.com/How_to_Simulate_a_Trebuchet_Part4.pdf

2. This is Earth’s escape velocity - or fast you need to be going in order to escape Earth’s gravitational pull.